Welcome to STAREVOL's lair

The IAA version of the Stellar Evolution code STAREVOL
STAREVOL is a one-dimensional Lagrangian hydrodynamic code (Henyey discretization scheme, Newton-Raphson relaxation algorithm) that uses as dependent variables the Lagrangian velocity u, the (log) radius lnr, lnf (a quantity related to the electron degeneracy), the (log) temperature lnT and the luminosity L. The relaxation of the equations is applied in one shot from the center to the surface (at some specified low optical depth).
The main papers describing the code are Siess et al (2000) and Siess (2006) for the constitutive physics Palacios et al (2006) for the treatment of rotational mixing and Siess & Arnould (2008) for the nuclear network.
Equation of State
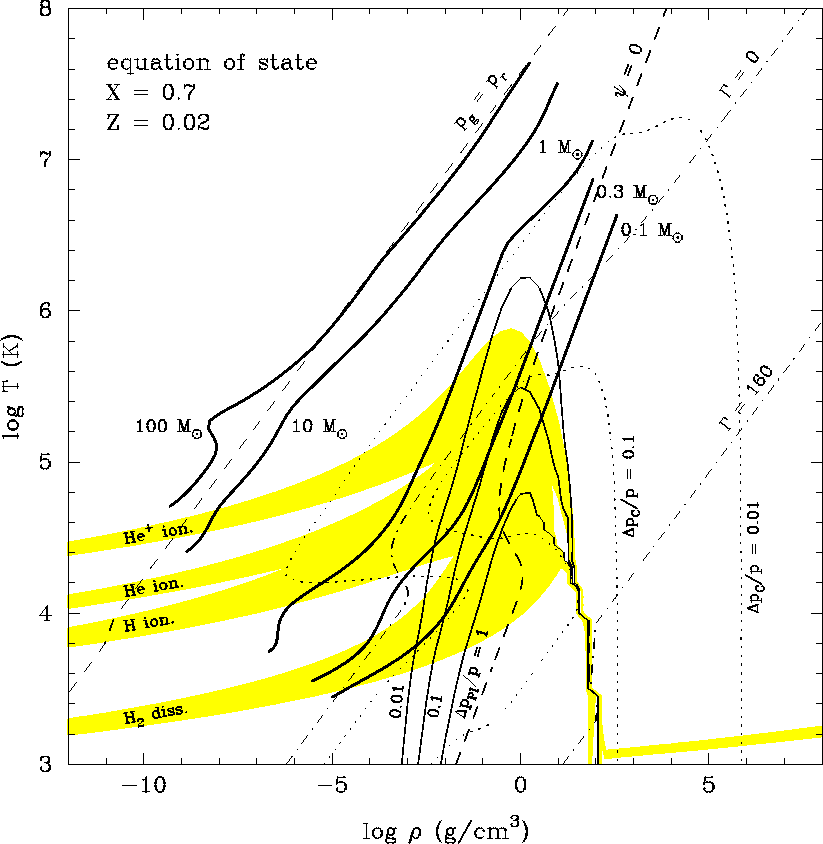
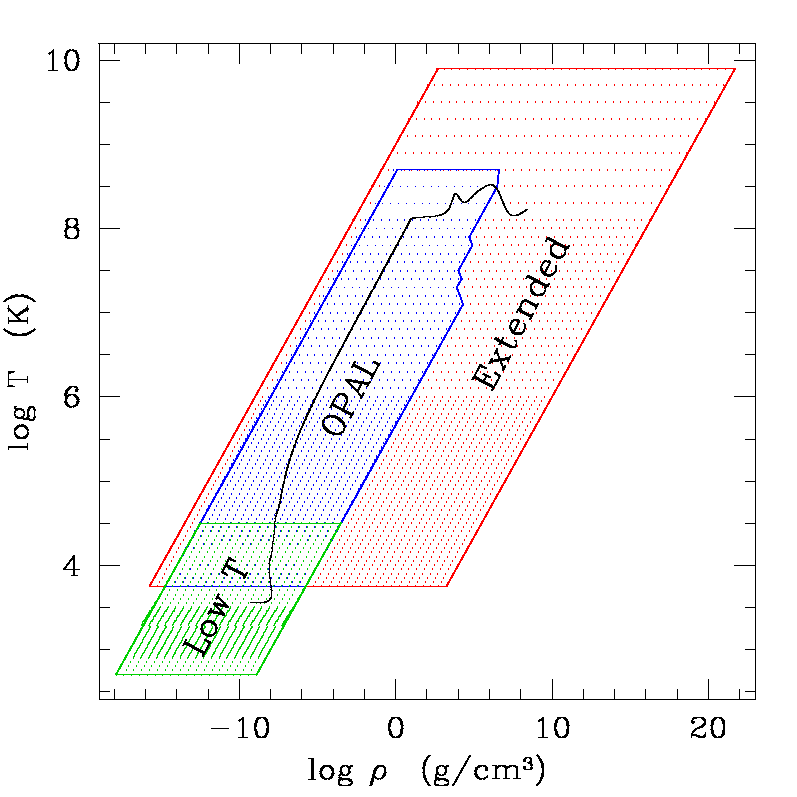
Based on the Pols, Tout, Eggleton, Zhanwen (1995, MNRAS 274, 964) equation of state: Helmholtz free energy minimization, consistent thermodynamics, plasma always considered as partially ionized and degenerate; a few parameters allow to treat (or not) partial ionization of C, N, O and Ne and to consider (or not) H- and/or H2. Effects of pressure ionization and Coulomb shielding have been incorporated by means of analytical fits to the non-ideal terms in the Helmholtz free energy. In practice, this expression provides a confident treatment of Coulomb interactions up to an interaction parameter Γ~ 300. The implementation and validation of this EOS can be found in Siess et al (2000).
Opacity
- radiative Rosseland mean opacities from Iglesias & Rogers (1996, ApJ 464, 943), including a new procedure to interpolate in Z tables corresponding to hot H-rich plasmas with enhanced C, N or O (implying the computation of tables enriched in Carbon and Nitrogen) and Ferguson et al. (2005, ApJ 623, 585) at low temperature
- conductive opacities from Hubbard & Lampe (1969, ApJS 163, 297), Iben (1975, ApJ 196, 525), Raikh & Yakovlev (1982, Ap. Sp. Sci. 87, 193), Itoh et al. (1983, ApJ 273, 774) and Mitake et al (1984, ApJ 277, 375)
- in the atmosphere of cool carbon rich stars (C/O>1), the effects of molecular opacities associated with H2, H2O, OH, C2, CN, and CO is taken into account following the procedure described in Marigo (2002, A&A 387, 507)
- in the regime of high temperature and density, opacities were extended using analytical fits
Nuclear Physics
- neutrino production rates from Itoh et al (1989, ApJ 339, 354)
- screening factors: formalism of Mitler (1977, ApJ, 212, 513)
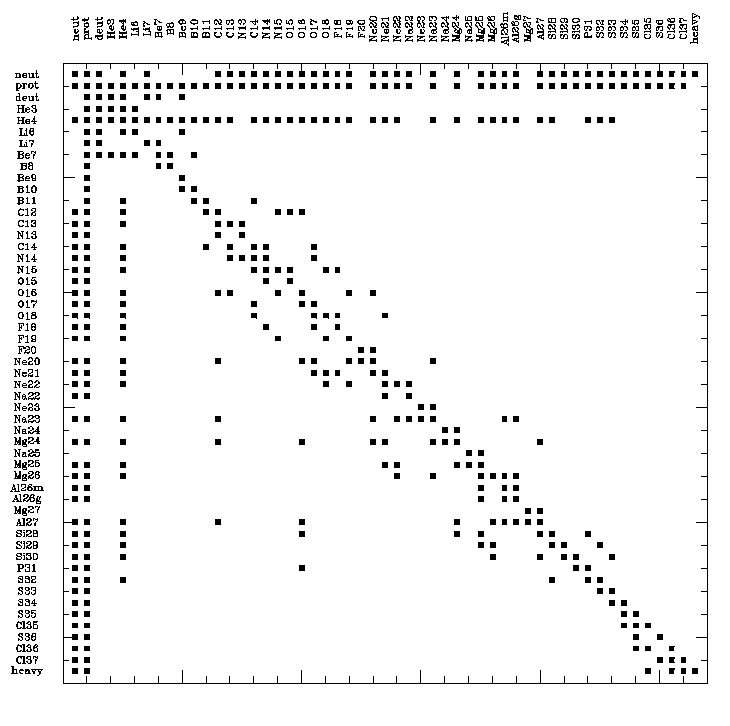
- the nuclear network inclide 53 species (n, 1,2H, 3,4He, 6,7Li, 8,10,11B, 7,9Be, 12,13,14C, 13,14,15N, 15,16,17,18O, 18,19,20F, 20,21,22,23Ne, 22,23,24,25Na, 24,25,26,27Mg, 26g,26m,27Al, 28,29,30Si, 31P, 32,33,34,35,36S, 35,36,37Cl, plus a fake element called Heavy that accounts for all the other species and 177 nuclear reactions that take all major nuclear (n-, p-, α-captures), weak (electron captures, β-decays) and electromagnetic (photodisintegration) interactions into account. The nuclear reaction rates are given by (1) Iliadis (2) NACRE or (3) Caughan & Fowler (1988).
Surface Boundary Conditions
- black body boundary conditions
- grey atmosphere (Eddington approximation)
- an analytic T($\tau$) relation, derived and fitted from various sophisticated radiative transfer models
Convection
- 2 different methods to solve the MLT equations for the convection treatment, possibility to use the density scale height instead of the pressure scale height, possibility to treat the turbulence from a simplified model
- time-dependent treatment of the convective mixing, through diffusion equations involving nuclear burning terms (with our full network or a reduced one, suited for the HBB occurring during the AGB phase for example), solved with a Newton-Raphson procedure
Mass Loss
different prescriptions for the mass loss rate (depending on the stellar mass and evolutionary stage) are implemented
Transport Processes
- treatment of angular momentum transport (Palacios et al. 2006, A&A, 453, 261)
- various transport processes for the chemical species can be considered :
- overshooting
- semi-convection
- thermohaline mixing
- atomic diffusion
- rotationally induced mixing (meridional circulation, shear and turbulent mixing)
Accretion
- Mass accretion can treated using a parametric hydrodynamical model taking into account the mechanical, thermal and chemical properties of the accreted matter (Siess, Forestini, 1996, A&A, 308, 472)
- the numerical treatment of accretion and mass-loss uses a pseudo-lagrangian variable as described by Neo et al (1977)
Hydrodynamics
artificial viscosity is used to model the propagation of shock waves